В.С. Зельцер

Матричный аппарат определения параметров функции с гибкой структурой для целей экстраполяции и аппроксимации

Для аппроксимации функции неизвестного вида или упрощения вида известной функции используются аппроксимирующие функции различных классов.

Используются также суперпозиции этих функций или иные комбинации, причем выбор структуры этих комбинаций, как и выбор классов функций, обычно осуществляется интуитивным путем.

При этом плохой выбор класса аппроксимирующей функции может привести, даже при хорошем совпадении функций в известных точках, к совершенно неверным выводам о поведении аппроксимирующей функции за пределами области известных значений.

Примерами могут служить экстраполяция синусоиды степенным многочленом, который, довольно хорошо аппроксимируя заданный участок синусоиды, быстро расходится с ней за пределами этого участка, т.к. может иметь только фиксированное число стационарных точек, или, наоборот, экстраполяция участка полиномиальной функции посредством ряда Фурье. Кроме того, плохой выбор класса аппроксимирующей функции может наложить существенные ограничения на точность аппроксимации при допустимой сложности аналитической записи функции.

Значительными преимуществами с этой точки зрения обладает введенная проф. Н.К.Куликовым т.н. функция с гибкой структурой (ФГС) [1], которая для одного аргумента может быть записана в виде

(1)

где x₀ - начальная точка,

n - порядок ФГС,

,

получается из D заменой r_j^k-1 на 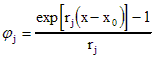для .

Являясь решением обыкновенного линейного неоднородного дифференциального уравнения с постоянными коэффициентами, ФГС хорошо приближает описываемые такими уравнениями зависимости, которые охватывают большинство встречающихся случаев.

В отдельных частных случаях ФГС может вырождаться в экспоненты, степенные, гиперболические иди тригонометрические многочлены и их комбинации, в частности, в ряды Эйлера и Фурье. Благодаря такой гибкости ФГС вопрос о выборе класса аппроксимирующей или экстраполирующей функции теряет остроту. После конкретизации параметров ФГС по ее виду можно установить, какие из обычно применяемых функций являются наиболее соответствующими представляемой зависимости и перейти к аналитическому выражению зависимости в виде этих функций. Единый характер преобразований, высокая точность приближения и чувствительность к особенностям приближаемой функции делают ФГС удобным средством для исследования различных зависимостей, в особенности с целью прогнозирования [2].

Для случаев, описываемых нелинейными или имеющими переменные коэффициенты дифференциальными уравнениями, имеются соответствующие обобщения ФГС (например, вводятся зависимости r_j=r_j(x)), однако даже в таких случаях ФГС с фиксированными r_j дает, как правило, хорошее приближение. В то же время постоянство r_j значительно упрощает вычисления и обозримость результатов, в связи с чем в дальнейшем рассматривается именно этот вид ФГС.

Приближение функции Z(x) функцией с гибкой структурой записывается в виде

, (2)

где ,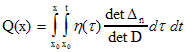

получаем из D заменой r_j^n-1 на для ,

- базисная функция.

Для наилучшего приближения Z(x) необходимо минимизировать Q(x), для чего следует положить базисную функцию равной нулю на всем интервале изменения аргумента, что приводит к линейному однородному дифференциальному уравнению

(базисное уравнение).

Разделив обе части на b₁, приводим базисное уравнение к виду

,

где , следовательно, a₁=1.

Положив z⁽¹⁾=y, имеем .

Характеристическое уравнение

.

Для нахождения коэффициентов a₂, ..., a_n+1 интегрируем (n+1) раз дифференциальное уравнение.

Тогда .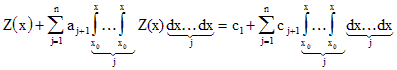

В этом уравнении c₁, ..., c_n+1 являются постоянными интегрирования.

Взяв x=x₀, находим

c₁=Z(x₀).

Используя формулу Коши

,

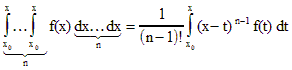получаем

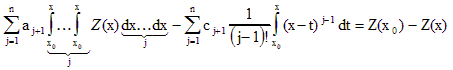
Взяв правый интеграл в левой части выражения, имеем

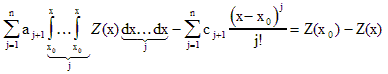(3)

Можно еще упростить это выражение, представив его в виде

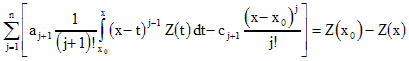
Однако с вычислительной точки зрения предыдущий вариант предпочтительней, так как повторный интеграл берется в численном виде с большей легкостью и точностью, чем интеграл со степенной функцией высокого порядка.

Повышение качества аппроксимации может быть в некоторых случаях достигнуто при использовании аппарата преобразований Тейлора [3].

Соотношение (3) может быть при введении оператора интегрирования 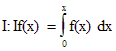переписано в виде

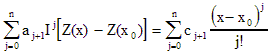(4)

Поскольку оно остается справедливым при любом n, очевидно, что равенство

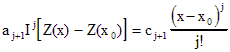
верно для любого j, что дает соотношение между коэффициентами одинакового порядка

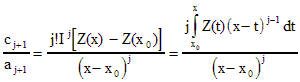
Определив c(j)=c_j+1 для всех , легко заметить, что правая часть (4) представляет собой результат обратного преобразования Тейлора от усеченного спектра производных (T_p-изображения) неизвестной пока функции C(t). Последнюю можно найти обратным T_p-преобразованием, однако таблицы обратного T_p-преобразования труднодоступны. Поэтому целесообразно перейти от T_p-изображения к обычному тейлоровскому изображению (T-изображению), для которого имеются готовые таблицы и формулы обратного T_p-преобразования [3].

T-изображение можно найти, пользуясь формулой

,

где C(j) - решетчатая функция T-изображения C(t),

H - произвольная постоянная.

В левой части (4), представляющей собой интегральный многочлен, также может быть выделен усеченный спектр производных, выраженный в виде решетчатой функции a(j) через совокупность a_j+1 посредством соотношения

a(j)=j!a_j+1

Тогда, рассуждая аналогично предыдущему, имеем

A(j)=H^ja(j),

где A(j) - T-изображение функции A(t).

Находя A(t)=T^-1[A(j)] и C(t)=T^-1[C(j)] по таблицам и формулам T-преобразования, часто удается установить функцию, хотя бы приближенно отражающую характер изменения a(j) и c(j) и, тем самым, коэффициентов a_j+1 и c_j+1 при возрастании j, что позволяет повысить точность аппроксимации функцией с гибкой структурой без производства трудоемких расчетов a_j+1 и c_j+1 высокого порядка, заменяя их более простым получением приближенных значений коэффициентов с помощью найденных функций.

В тех случаях, когда не удается подобрать хорошее аналитическое выражение функций A(t) и C(t) по их T-изображениям, можно воспользоваться известной методикой продолжения степенных рядов для уточнения T-изображений, в связи с чем отпадает необходимость в явном выражении A(t) и C(t). Можно отметить также возможность рекурсивного применения данного метода для экстраполяции решетчатых функций a(j) и c(j) с целью повышения качества аппроксимации.

При проведении последовательных повторных интегрирований заданной таблично функции встает вопрос о выборе вида применяемых формул численного интегрирования.

Применение квадратурных формул эквивалентно аналитическому (точному) интегрированию при интерполяции графика функции отрезками парабол заданного, зависящего от конкретной формулы, порядка. Поэтому повторное интегрирование с использованием квадратурных формул приводит при большом числе повторений к значительным ошибкам. Например, линейная функция превращается при интегрировании в параболы все более высоких порядков, что при ограниченном порядке квадратурной формулы ведет к появлению и росту погрешностей.

Для уменьшения ошибок такого рода целесообразно использовать сплайн-интерполяцию с последующим интегрированием по специальным формулам, вид которых меняется в зависимости от номера шага последовательного интегрирования.

При неизвестном ходе функции в промежутках между опорными точками сплайн, как известно, реализует наиболее "естественную" гладкую функцию на множестве непрерывных функций, проходящих через опорные точки. Повышение порядка сплайна до некоторого предела ведет к повышению точности интегрирования, однако сплайны слишком большого порядка начинают навязывать аппроксимирующей функции свою структуру. Можно рекомендовать использовать, в зависимости от числа опорных точек и порядка функции с гибкой структурой, сплайны с порядками от 1 (кусочно-линейная функция) до 3.

Формула для m-го интегрирования в случае интерполяции линейными сплайнами (кусочно-линейными функциями) имеет на каждом отрезке [x_i, x_i+1] между двумя соседними опорными точками следующий вид

, (5)

где

Видно, что в каждой точке x_i необходимо вычислить последовательно значения , после чего результат интегрирования на отрезке [x₁, x₂] можно будет найти по формуле (5).

Для нахождения значения интеграла на всем интервале интегрирования остается только просуммировать интегралы по входящим в него отрезкам.

Взяв 2n опорных точек, можно составить систему уравнений и решить их, находя a_j и c_j для .

Записывая эту систему уравнений в матричном виде, имеем

LG=Z, (6)

где ,

,

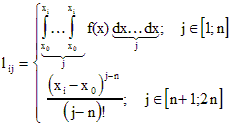
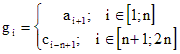
Из (6) находим

G=L^-1Z

Погрешность приближения функции мала в окрестности начальной точки x₀ и увеличивается при удалении от нее. В связи с этим начальную точку целесообразно выбирать вблизи или на краю интервала экстраполяции.

Погрешность приближения имеет две составляющие: погрешность за счет неточности вычисления интегралов и погрешность за счет ограниченности порядка приближения, ведущегося по опорным точкам. Среднее значение второй составляющей можно снизить и сделать эту составляющую более равномерной по интервалу изменения аргумента ФГС, использовав для нахождения вектора коэффициентов G метод наименьших квадратов [4]. В этом случае матрица L имеет размерность m*2n, а G находится по формуле

G=(L^TL)^-1L^TZ

Однако при более важном значении точек, близких к начальной, использовать эту формулу нецелесообразно, т.к. в этой области точек точность аппроксимации может ухудшиться.

Подставив найденные значения a_j и c_j в проинтегрированное базисное уравнение и снова продифференцировав его, можно найти Z^(j)(x₀).

Практически удобнее решить систему алгебраических уравнений

,

где

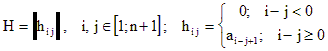
Подставив в характеристическое уравнение полученные значения, находим его корни . При представлении ФГС в виде (1) каждый член разложения представляет собой сумму нескольких экспонент, зависящих от x. Возможно, однако, преобразовать формулу к более удобному и обозримому виду, разлагая по и проводя перегруппировку коэффициентов

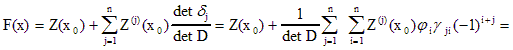
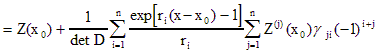
где - минор соответствующего элемента в .

Теперь при представлении ФГС в аналитическом виде можно заранее вычислить коэффициенты ряда при 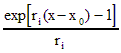, благодаря чему становится виден вклад каждой экспоненты и упрощаются вычисления.

При группировке членов следующим образом

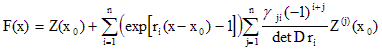
видно, что полученное выражение можно представить в матричной форме следующим образом

,

где

Вычисление R^-1 можно оптимизировать, учитывая, что R по виду близка к матрице Ван-дер-Монда, благодаря чему расчет элементов R^-1 значительно упрощается по сравнению с общим случаем [5, стр.67].

Воспользовавшись этим, можно записать

,

где

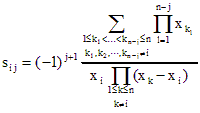
Выражение в числителе может быть также вычислено с помощью операций над многочленами, поскольку оно равно коэффициенту при x^j-1 в многочлене .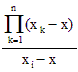

Представив вектор в виде разности векторов

где

можно преобразовать (1) к виду

,

где

Некоторые компоненты вектора K могут быть комплексными, при этом они будут составлять комплексно-сопряженные пары, например, r_j и r_j+1. При этом k_j и k_j+1 будут равны вследствие действительности получаемой функции. Поэтому можно записать результат в действительном виде, используя соотношение

При замене по данной формуле членов с комплексными экспонентами на функции действительного переменного получается для каждого конкретного случая простая и удобная для практических приложений форма окончательной аналитической записи ФГС.

Проведенные выкладки были ориентированы на получение формул в виде, удобном для программирования на ЭВМ. Как было показано, при нахождении параметров ФГС легко реализуется матричный аппарат вычислений, что обеспечивает компактность получаемой программы и широкое использование стандартных подпрограмм.

Описанная схема вычислений допускает обобщение на многомерные случаи, при этом целесообразным представляется запись преобразований с использованием многомерных матриц [7], операции с которыми легко реализуются в распространенных языках программирования.

Получаемая описанным методом аппроксимирующая функция обеспечивает хорошие результаты при экстраполяции и интерполяции, в особенности когда искомые точки лежат вблизи от начальной, а также при поиске периодических составляющих, тренда и т.п., поскольку вся соответствующая информация явно отражается в получаемой аналитической записи ФГС. Аппроксимирующая ФГС в общем случае не соответствует критерию минимации невязки методом наименьших квадратов, однако при необходимости может быть впоследствии откорректирована в соответствии с этим критерием при использовании подходящей итерационной процедуры (см. например, [8]), исходные данные для которой находятся из приведенных соотношений. В частности, при задании числа точек, в которых вычисляется невязка, равным порядку ФГС, аппроксимирующая ФГС будет проходить через эти точки, что представляет интерес в ряде практически встречающихся случаев.

Таким образом, использование матричного аппарата определения параметров функции с гибкой структурой позволяет в компактной и пригодной для программной реализации форме представить необходимые для определения ее параметров формулы.

Литература

1. Куликов Н.К. Обобщенная формула для представления функций. М., МТИПП, 1970
2. Куликов Н.К. Математическое моделирование результатов экспериментов и прогнозирование на основе функций с гибкой структурой. М., МТИПП, 1974
3. Пухов Г.Е. Преобразования Тейлора и их применение в электротехнике и электронике. Киев, "Наукова думка", 1978
4. Кади Дж. Количественные методы в экономике. М., "Прогресс", 1977
5. Кнут Д. Искусство программирования на ЭВМ. т.1. М., "Мир", 1976
6. Араманович И.Г. Математический анализ. М., Государственное издательство физико-математической литературы, 1961
7. Соколов Н.П. Введение в теорию многомерных матриц. Киев, 1972
8. Надпорожская Е.В., Егоров С.К. Библиотека процедур на языке ИНФ. Л., "Наука", 1975